1、简介

本笔记记录许多在统计学、信息处理（数字信号处理、时间序列模型等）中常用的一些方法和概念，同时使用python3实现。

2、统计量和信息处理方法

2.1 统计量

基本

标准差、平均值、最大值、最小值、中位数等基础

q位数(qth-quantile)

将数据按照大小平均分为q份。

# 至少有0.95的数据小于等于返回的q位数，(1-0.95)的数大于等于
numpy.quantile(data, 0.95)
# 至少有95%的数据小于等于返回的q位数，(100-95)%的数大于等于
numpy.percentile(data, 95)

差分(difference)

# data的一阶差分
numpy.diff(data)
# data的二阶差分
numpy.diff(data,n=2)
# data的一阶差分率
numpy.diff(data)/data[:-1]

平均绝对偏差(mad,mean absolute deviation)

data = pandas.Series(...)
data.mad() # 平均绝对误差

峰度(kurtosis)

数据分布陡峭或平滑的统计量，通过对峰度系数的测量，我们能够判定数据分布相对于正态分布而言是更陡峭还是平缓。

data = pandas.Series(...)
data.kurtosis()  # 返回峰度

偏度(skewness)

数据分布对称程度的统计量

data = pandas.Series(...)
data.skew()  # 返回峰度

置信区间

均值的±(N*标准差)，其中N一般为1,2,3

2.2 信息处理方法

希尔伯特变换(hilbert transform)

将一维数据转化为复平面数据a+bj

scipy.signal.hilbert(data)

卷积

scipy.signal.convolve(data)

窗函数

除在给定区间之外取值均为0的实函数，可以用于防止信号频谱泄露。

• hann窗口

  离散型窗函数w(n) = (sin(pi\*n/(N-1)))^2，其中窗口的长度为N+1，n为0到N-1整数。见下图hann函数和傅里叶变换。时域卷积=频域相乘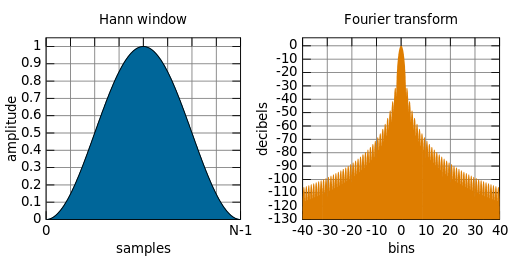

  

滚动窗口

滚动区间选取数据进行计算

data = pandas.Series(...)
data.rolling(window=700).mean().mean(skipna=True)

指数加权函数(ewf,exponential weighted functions)

alpha*V+(1-alpha)*theta

pd.Series.ewm()

2.3 统计可视化

QQ图

全称quantile-quantile plot，横坐标理论值，纵坐标采样值。

• 正态分布QQ图

  横坐标：标准正态分布的分位数

  纵坐标：样本值

3、数学背景

3.1 概率

• 先验概率

事件发生前的预判概率。可以是基于历史数据的统计，可以由背景常识得出，也可以是人的主观观点给出。一般都是单独事件概率，如P(x),P(y)。

• 后验概率

事件发生后求的反向条件概率；或者说，基于先验概率求得的反向条件概率。概率形式与条件概率相同。

• 条件概率

一个事件发生后另一个事件发生的概率。一般的形式为P(x|y)表示y发生的条件下x发生的概率。

• 贝叶斯公式实例

公式：P(y|x) = ( P(x|y) * P(y) ) / P(x)

P(y|x) 是后验概率，一般是我们求解的目标。

P(x|y) 是条件概率，又叫似然概率，一般是通过历史数据统计得到。一般不把它叫做先验概率，但从定义上也符合先验定义。

P(y) 是先验概率，一般都是人主观给出的。贝叶斯中的先验概率一般特指它。

P(x) 其实也是先验概率，只是在贝叶斯的很多应用中不重要（因为只要最大后验不求绝对值），需要时往往用全概率公式计算得到。

实例

假设y是文章种类，是一个枚举值；x是向量，表示文章中各个单词的出现次数。

在拥有训练集的情况下，显然除了后验概率P(y|x)中的x来自一篇新文章无法得到，p(x),p(y),p(x|y)都是可以在抽样集合上统计出的。

3.2 分布函数和概率密度

F(x) = P{X<x}

F(x)：分布函数；P(x)：概率密度

欢迎关注我的微信公众号

互联网矿工